어떤 연립방정식이 다음과 같이 주어졌을 때,

이를 행렬의 곱 Ax = b 형태로 다음과 같이 표현할 수 있다.

위 행렬을 Gauss Elimination (가우스 소거법)을 이용하여,
A를 Upper triangular matrix인 row echelon form 형태로 정리하면 연립방정식의 해를 얻을 수 있다.
그 과정은 다음과 같다.
1. Pivoting : 기준이 되는 각 행의 첫 요소가 가장 큰 절댓값을 가지도록 행을 변경하는 과정
기준 행인 1행의 첫 요소가 가장 큰 절댓값을 갖도록 행을 바꾸어준다.

2. Forward Elimination : Pivot이 설정된 기준 행과 열에 대하여 기준 행을 제외한 기준 열의 요소를 0으로 정리한다.



위 1, 2 과정을 Upper Triangular matrix (diagonal line(대각선) 아래의 모든 요소가 0)가 될 때까지 반복한다.
다음 Pivot은 2행 2열이 되어, 기준 행과 열도 마찬가지로 2행 2열이 된다.
동일하게 Pivot이 있는 행을 이용하여 아래 행의 모든 열을 0으로 만들어준다.




4x4 행렬에서 Pivoting과 Forward Elimination의 마지막 반복 과정




Upper Triangular matrix 가 완성되었다.
3. Back Substitution : Upper Triangular matrix로 부터 해를 얻는 과정
맨 아래 행부터 각 해를 구할 수 있다.
0.4568423x4 = 0.89158203 이므로,
x4= 0.89158203/0.4568423 이다.
또한, x4를 이용하여 x3를 계산할 수 있다.
5.50407747x3 -1.59150527x4 = 0.9951291
x3 = (0.9951291 - (-1.59150527x4))/5.50407747
차례로 x1까지 구할 수 있다.
1번 과정인 Pivoting은 필수는 아니지만,
Gauss Elimination을 통해 Gauss elimination 연립방정식을 해결하면,
계산 도구(계산기, 컴퓨터)를 사용하는 경우에서 round off 가 발생할 수 있다.
예를 들어
0.0003x1 + 3.0000x2 = 2.0001
1.0000x1 + 1.0000x2 = 1.0000
와 같은 연립방정식을 Gauss Elimination으로 정리할 때,
두 번째 행을 Forward elimination 하기 위해서는
첫 번째 행에 1.0000/0.0003 을 곱하여 두 번째 행을 정리한다.
그러나 이 때, 첫 번째 행의 각 값에 1.0000/0.0003 이라는 매우 큰 수를 곱하게 되는데
이는 메모리에서 길이가 긴 수를 다뤄야하는 문제가 발생하여,
기기 한계에 따라 round off가 발생할 수 있다.
또한, 곱해주는 값이 크다보니 machine epsilon 에 의한 에러도 크게 발생한다.
컴퓨터에서 숫자 1이 완벽한 1.0000000000000000000
이 아닌 1.0000000000000011102... 으로 저장되기 때문이다.
machine epsilon에 관해서는 다음 글을 참조하기 바란다.
[수치해석] Python을 이용한 Machine epsilon(한계 오차) 계산
컴퓨터는 숫자를 저장할 때 2진법으로 저장한다. 따라서, 입력 받은 숫자를 2진법으로 저장하고, 저장된 숫자를 다시 10진법으로 변환하여 출력하는 과정을 거친다. 당연하게도 숫자 하나를 저장
cobang.tistory.com
따라서 이러한 문제를 Pivoting을 수행하여
machine epsilon에 의해 발생하는 오차를 줄인다.
그렇다면 위와 같은 과정을 어떻게 코드로 구현할 수 있을까?
먼저 연산 과정을 살펴보고 구현해보도록 하겠다.
1. Pivoting
linear search를 통해 target 열의 절댓값이 가장 큰 값을 target 행 위치와 변경한다.
2. Forward Elimination
아래와 같은 행렬이 있다고 하자

이 행렬을 첫 번째 Forward Elimination 하기 위해 다음과 같은 연산을 수행한다.

각 반복 시 마다 pivot 행 아래에 남은 행의 개수만큼 반복 연산한다.
동일한 연산을 b에도 마찬가지로 해줘야한다.
이 원리를 이용하여 작성한 코드는 다음과 같다.
import numpy as np
A=np.array([[0.3,0.2,6.6,-1.1],
[4.5,-1.8,-0.3,6.5],
[-7.3,9.7,10.9,-4.1],
[8.1,-2.7,8.7,8.9]])
b=np.array([[1.0],[0.1],[0.01],[0.001]])
x=np.empty((len(A),1))
for i in range(len(A)-1):
# Pivoting
# Find the maximum value
max=A[i][i]
max_row=i
for j in range(i+1,len(A)):
if max<abs(A[j][i]):
max=abs(A[j][i])
max_row=j
# Scaling : Bring the maximum row to the top
if max_row!=i:
A[[i,max_row]]=A[[max_row,i]]
b[[i,max_row]]=b[[max_row,i]]
#Forward elimination
for j in range(i+1,len(A)):
if A[j][i]!=0:
c=A[j][i]/A[i][i]
for k in range(i,len(A)):
A[j][k]=A[j][k]-c*A[i][k]
b[j]=b[j]-c*b[i]
위 코드는 메모리 영역 내의 계산이라면 4x4가 아닌 n x n 행렬에 대하여도 수행 가능하다.
위 과정을 마치면 다음과 같은 행렬을 얻게 된다.


이어서 3. Back Substitution
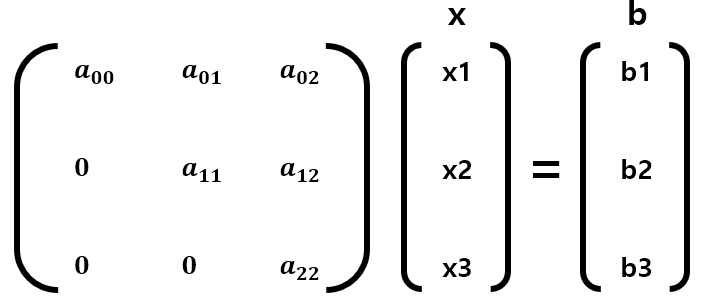
위와 같이 정리된 행렬에서 마지막 행부터 해를 계산한다.
#Back substitution
for i in range(len(x)):
#Calculate x from the last row
x[len(x)-1-i]=b[len(x)-1-i]/A[len(x)-1-i][len(x)-1-i]
#using the lower x for new x
for j in range(i):
if A[len(x)-1-i][len(x)-i+j]!=0:
x[len(x)-1-i]-=A[len(x)-1-i][len(x)-i+j]*x[len(x)-i+j]/A[len(x)-1-i][len(x)-1-i]
#print {x}
print("x\n", x)
전체 코드는 다음과 같다.
결과로 얻은 해는 다음과 같다.

'Research & Algorithm > 수치해석' 카테고리의 다른 글
| [수치해석] Python을 이용한 수치 미분과 Taylor series expansion을 이용한 오차 분석 (2) | 2023.01.08 |
|---|---|
| [수치해석] Python을 이용한 Machine epsilon(한계 오차) 계산 (0) | 2023.01.06 |
| [C++] Get area using Monte Carlo method (0) | 2022.10.01 |
| [C++] Integration with the Area of Rectangle and Trapezoid (1) | 2022.09.16 |