[수치해석] Python을 이용한 수치 미분과 Taylor series expansion을 이용한 오차 분석

어떤 함수 f(x)가 다음과 같이 주어진다고 하자.

해당 함수의 도함수는 다음과 같을 것이다.

 

만약 컴퓨터에서 기존 함수에 대해 미분을 한 도함수를 얻고, 계산하고 싶을 때,

컴퓨터는 도함수를 어떻게 유도해낼 수 있을까?

 

안타깝게도 컴퓨터는 함수로부터 이러한 도함수를 유도 해낼 수 없다.

(컴퓨터가 다양한 함수의 도함수를 학습을 통해 얻지 않은 경우라고 가정)

대신 컴퓨터는 계산이 매우 빠르기 때문에, 근사를 통해 해당 도함수와 최대한 유사하게 표현할 수 있다.

 

즉, 어떤 점 x_i 에서의 미분 계수를 컴퓨터에서는 x_i와 x_i+1 사이의 h를 매우 작게 계산하여 유도할 수 있다.

출처 : Steven C. Chapra, Raymond P. Canale - Numerical Methods for Engineers 7th edition

고등학교 때 배우는 미분 계수의 정의를 생각해봐도 쉽게 이해할 수 있을 것이다.

 

그러나 이러한 식은 Taylor series expansion에서 오차항을 무시하고 유도된 결과이다. 

테일러 급수를 이용하여 x_i로 부터 h, 2h만큼 떨어진 x_i+1, x_i+2, x_i-1, x_i-2 점의 함수 값을 계산할 수 있다.

 

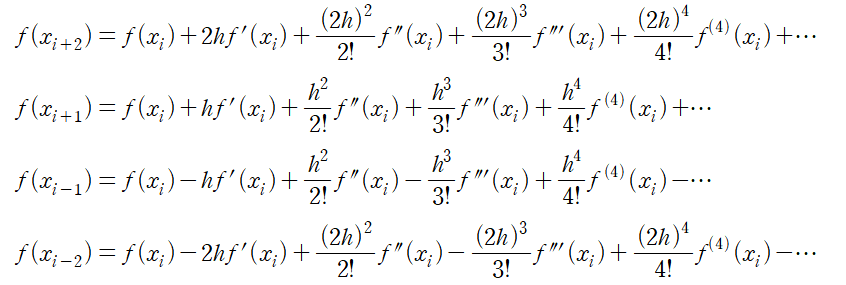
가장 간단한 예로, 2번째 식을 이용해서 미분 계수 함수 형태로 정리하면, 

위와 같이 정리되고, 기존의 미분계수 식에 더하여 빨간 밑줄로 h에 관한 1차식을 포함한 f''(x) 이상의 항이 추가되었음을 확인할 수 있다.

우리가 목표한 항 f '(x_i) 을 초과한 미분 항은 필요로 하지 않는다. 

따라서 이 항들은 error 항이 된다.

Error 항 중 가장 낮은 h 차수를 이용하여 Error의 차수를 표현하며, 

위 식은 h에 대하여 1차식이 가장 낮은 차수이므로 1st order accuracy를 가진다. 

가장 낮은 h를 찾아 order를 붙이는 이유는 가장 낮은 차수의 h가 error의 크기에 가장 큰 영향을 미치기 때문이다. 

 

그렇다면 기존 함수를 한번 미분한 도함수에 대하여 미분 계수는 언제나 1st order accuracy를 가지는가?

그것은 아니다.

출처 : Steven C. Chapra, Raymond P. Canale - Numerical Methods for Engineers 7th edition

위와 같이 미분계수를 계산하는 구간을 잡고 Taylor series expansion을 정리해보면,

여러 항이 소거되고 2h로 나누어지면서 2nd order accuracy가 되는 것을 확인할 수 있다.

x_i+2, x_i-2 항이 더 추가되면 accuracy는 더 높아질 수 있다.

 

그렇다면 위와 같이 h를 작게 하여 미분계수를 구하는 방식으로는 필연적으로 error가 발생함을 이해할 수 있다.

근사를 통해 미분계수를 구하는 방식은 정확한 도함수의 함수값과 차이가 발생하는 것이다.

그리고 해당 차이(오차)는 미분 계수를 계산한 방식에 따라 order가 결정된다. 

 

Error의 차수에 따라 h값이 커지고 작아지는 것에 따라 차이가 발생하게된다.

1st order accuracy는 grid space인 h 값이 1/2 이 되면 error도 1/2 이 된다.

2nd order accuracy는 h 값이 1/2 이 되면 error는 1/4이 된다.

3rd order accuracy는 h 값이 1/2 이 되면 error는 1/8 이 된다.

그렇다면 n th order accuracy의 h 값이 1/2가 되면 error는 어떻게 될까?

 

그렇다. 1/(2^n) 이 될 것이다.

 

그렇다면 처음으로 돌아가서 주어졌던 함수를 Python 코드를 작성하여 x=0 일 때의 실제 도함수 값과 error를 비교해보자.

 

위에서 언급한 아래 두 가지 method를 이용할 것이다.

편의를 위해 위의 것을 a, 아래 것을 b라고 하자.

 

Code

 

Explanation

f(x)와 참값 비교를 위한 도함수 f '(x) 를 만들고,

위에서 언급한 두 가지 방법 a (x_i+1 과 x_i  이용 : 1st order accuracy),

b (x_i+1과 x_i-1 이용 : 2nd order accuracy) 를 Error 항을 제외하고 함수를 만든다.

그리고 Error 항의 크기를 계산하는 getError 함수를 만든다.

그리고 두 가지 grid space인 1/40과 1/80에 대하여 참값과 수치미분 함수 값 사이의 error를 비교한다.

 

Result

1st order accuracy인 method a는 grid space h가 절반이 되니, 동일하게 error도 절반으로 줄었다.

2nd order accuracy인 method b는 h가 절반이 되니, errror는 1/4 로 줄었다.

이는 위에서 말한 error항의 h 차수에 따른 accuracy 분석과 일치하는 결과이다.

 

또한, 2nd order accuracy의 method를 이용했을 때 참값과 더 가까운 수치 미분값이 나타나는 것도 확인할 수 있다.

이는 Error 항 차수가 높은만큼 수치 미분값 자체가 더 정확한 값을 가진다는 의미이다.